Updated:
Keep
Taking advantage of the extra time that the Christmas holidays allow, I decided to read a beautiful book that had been waiting for me for a long time: ‘Mathematics and Literature’ by the brilliant mathematician and popularizer Marta Macho Stadler.
This book, which I highly recommend, delves into the relationships that exist between these two disciplines, normally considered very distant both in content and in their work techniques. However, as can be seen throughout the reading of it, there are not a few occasions in which literature drinks from contents of mathematics; both for its plots, generally in mystery or police novels, and in the use of numerical structures that must comply with certain rhymes, such as, for example, sestinas.
On the other hand, in terms of work methodology, mathematics and literature tend to be seen as intellectual activities with tremendously different characteristics. However, as the author herself expresses, and a server shares, they are not as far apart as we usually believe: «The majority perception is that mathematics is cold, it is deduced from established rules and leaves little room for imagination. It is also thought that literature arises exclusively from creativity, inspiration, emotion. But nevertheless, […] mathematics requires large doses of ingenuity and intuition. […] And in literature, the letters do not arise solely from creative impulses; it is necessary to plan and structure so that a good story translates into a good text». (Male Stadler, 2021, p.9).
Despite what it may seem, this week’s entry in the ABCdario of Mathematics is not going to deal with the relationship between mathematics and literature, but rather with a specific example found in Macho Stadler’s book that relates both disciplines: the crime novel. ‘Who a tué le duc de Densmore?’ (Who Killed the Duke of Densmore?) by the writer and mathematician Claude Berge. In this novel a crime is related that is solved by a mathematician without more than using a specific branch of mathematics, graph theory.
Let’s talk a bit regarding graph theory
Graph theory is a branch of mathematics that is dedicated to the study of the properties and results related to objects known as graphs. But what is a graph? A graph G is a set formed by two types of objects: vertices V and edges E, where the latter are actually pairs of vertices.
Thus, a graph G = (V, E) can be described through the vertices and edges that form it. For example, a graph G 1 = (V, E) can be expressed by determining its vertices V = {a, b, c, d} and its edges E = {(a,b), (a,c), (a,d ), (b,d)}. Similarly, this graph can be represented graphically by drawing each vertex as a point and each edge as a segment joining two vertices; in this way two graphical representations of G 1 would be:
Note that any continuous deformation applied to the representation of the graph is also a representation of the same graph, as long as the connections between the vertices are maintained.
Graph theory is one of those branches of mathematics whose importance goes beyond mathematics since its objects of study -graphs- serve to model situations from different disciplines such as chemistry, transport, biology, social networks, information and communication, circuits and networks. of computers among others. But can the study of graphs help us solve a crime?
A crime solved using graph theory
As described in Claude Berge’s novel, two Scotland Yard policemen try to solve a crime that occurred on the Isle of White. Two dead have appeared on that island:
Jeremy Morse -Duke of Densmore- and his butler Stewart. From the first moment the butler is suspected -a classic where they exist-, but anyway the police investigate all the people who have passed through the island in the last year without being able to determine the guilt of any of them. Later one of the policemen meets a mathematician colleague. After describing this event and the statements of the suspects, the mathematician draws a graph in which each person is represented by a vertex and each drawn edge represents the fact that the two people joined by said edge have coincided on the island. This graph drawn by the mathematician is what is known as a graph of intervals and using some of its properties, he is able to find out that one of the suspects should have coincided with more people on the island, a fact that indicates that some time has actually passed. periods hidden on the island, moments that she has actually used to prepare her macabre murder.
interval graph
If we represent several intervals on a real line, for example, we can think of the periods of time that certain people have spent on an island (see figure 3). The graph of these intervals is the one that is obtained by drawing a vertex for each interval or person, and two vertices will join with an edge if the people they represent have coincided on the island or what is the same if the corresponding intervals intersect ( see figure 3).
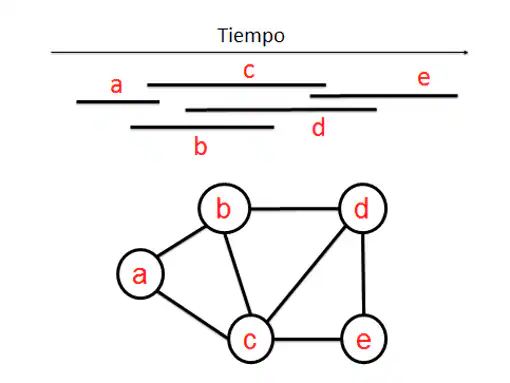
Interval graphs have interesting properties, some of which appear in Berge’s novel and allow the mathematician in the play to solve the crime. Today we will focus on the following:
An interval graph is always triangulated.
A graph is said to be triangulated if for every closed path (set of consecutive edges that begins and ends at the same vertex) formed by at least four edges, there is at least one that joins non-consecutive vertices (see Figure 4).
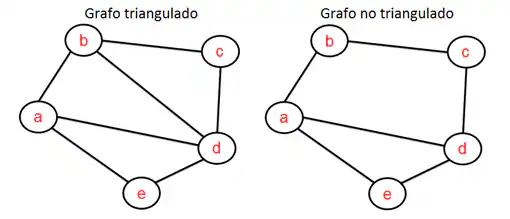
The proof of this property will not be presented here, but can be found in textbooks on graph theory. However, an informal justification for it is easy to come up with.
If we suppose that there is a graph of intervals with a closed path of length four and that it is not triangulated, when trying to construct the corresponding intervals that give rise to said graph we see that such a graph cannot exist (see figure 5).
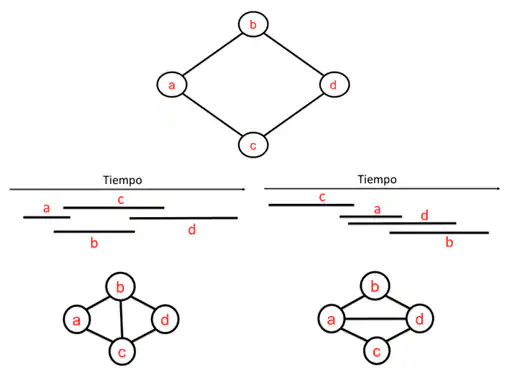
Knowing these brushstrokes of graph theory, the intrepid reader is challenged to become a mathematical inspector to solve the following crime.
A new crime to solve
Spring had just arrived and the veteran inspector Alicia Pelegrina of the National Police found herself facing a landscape plagued with snow. At his side, his young assistant, agent Jorge Martín. Despite her years of experience, Inspector Pelegrina had never seen a case like it. A woman, Araceli, had been found dead in the house she lived in in an abandoned town in the Aragonese Pyrenees where she was the only inhabitant. The investigations allow agents Pelegrina and Martín to conclude that the crime occurred due to a poisonous gas leak triggered by a timer. The device, which had been carefully installed, was hidden in the vicinity of the house and directed the lethal gas through a tube to it. The first investigations allow the agents to deduce that the crime has been carried out by a single person, but who?
Throughout the winter several people had visited the deceased, specifically 8. These are considered suspicious from the outset. Due to the intense snow, all the visitors had accessed the town from the only possible access, the Canfranc train station. The security guard at the station recalls seeing the 8 suspects on exactly two occasions, once on their way in and once on their way out, confirming that each suspect visited the victim only once. However, the guard does not remember the exact dates of each of them.
The list of suspects is as follows:
Laura Díaz (children’s book writer), Inés Mármol (punk group singer), Javier Fernández (comedian/screenwriter), Ramón Nogueras (climate activist), Daniel Pellicer (professional golf player), Pablo Tristán (renowned chef) , Alejandro Sánchez (violinist) and Maja Wrzeistein (professor of Hispanic literature).
In the interrogations, the suspects do not know how to specify the exact dates on which they were in the house of the deceased, but they are able to clearly describe the agents with whom they coincided:
– Laura claims to have coincided with Javier and Maja.
– Inés claimed to have seen Ramón and Pablo.
– Javier remembers seeing Laura, Alejandro, Daniel and Ramón.
– Ramón comments having seen Inés and Javier.
– Daniel remembers seeing many people, specifically Javier, Alejandro, Pablo and Inés.
– Pablo says he only saw Inés, Alejandro and Daniel.
– Maja comments that she only saw Laura and Alejandro.
The inspectors observe that the versions of the suspects do not present contradictions and in principle it does not seem that anyone is lying, or maybe they are?
In this new entry in the ABCdario of mathematics, the intrepid reader is challenged to solve this crime using graph theory. Would you be able to determine who is guilty of this crime?
NOTE: next week the solution to the enigma of the Alhambra prophecy will be explained in detail, and the present one, the next. In this way, the reader has fifteen days to quietly meditate on their answers.

Víctor M. Manero (@pitimanero) is a professor at the University of Zaragoza and a member of the Dissemination Commission of the Royal Spanish Mathematical Society (RSME).
.

